
แจกแนวข้อสอบ ช่างเครื่องกล องค์การเภสัชกรรม
แนวข้อสอบคณิตศาสตร์ (ความสามารถทางด้านตัวเลข)
ความรู้ความสามารถทางด้านตัวเลข (Number)
1. 27, 32, 39, 48, 59, ..................
ก. 69 ข. 67
ค. 70 ง. 72
ตอบ ง. 72 เป็นอนุกรมแบบธรรมดา
วิธีคิด 27 32 39 48 59 (72)
+ 5 + 7 + 9 + 11 + 13
2. 108 43 100 39 92 ...............
ก. 84 ข. 35
ค. 86 ง. 72
ตอบ ข. 35 เป็นอนุกรมเว้นระยะ แบบตัวเว้นตัว
วิธีคิด
108 43 100 39 92 (35)
3. 45, 33 , 22, 12, 3, ..................
ก. 1 ข. - 3
ค. - 4 ง. - 5
ตอบ ง. - 5 เป็นอนุกรม 2 ชั้น
วิธีคิด 45 33 22 12 3 (- 5)
- 12 - 11 - 10 - 9 - 8
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
+ 1 + 1 + 1 + 1
4. 3, 5 , 11, 29, ...............
ก. 83 ข. 105
ค. 43 ง. 47
ตอบ ก. 83 เป็นอนุกรม 2 ชั้น
วิธีคิด 3 5 11 29 (83)
2 6 18 54
![]()
![]()
![]()
![]()
![]()
![]()
![]()
x3 x3 x3
5. 45045 3465 315 35 ...............
ก. 3 ข. 5
ค. 7 ง. 9
ตอบ ข. 5 เป็นอนุกรม 2 ชั้น
วิธีคิด 45045 3645 315 35 (5)
¸ 13 ¸ 11 ¸ 9 ¸ 7
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-2 -2 -2
![]() 6. Ö3 3 9 .......
6. Ö3 3 9 .......
ก. 18 ข. 81
ค. 36 ง. 45
ตอบ ข. 81 เป็นอนุกรมยกกำลัง
![]() วิธีคิด Ö3 3 9 (81)
วิธีคิด Ö3 3 9 (81)
ยกกำลัง 2 ยกกำลัง 2 ยกกำลัง 2
7. 11 7 4 3 1 2 .......
ก. 0 ข. 1
ค. -1 ง. 2
ตอบ ค. -1 เป็นอนุกรมสะสมด้วยการลบ
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() วิธีคิด
วิธีคิด
![]()
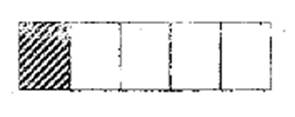
![]()
![]()
![]()
![]()
![]()
![]() 11 7 4 3 1 2 (-1)
11 7 4 3 1 2 (-1)
8. 25 35 75 135 .......
ก. 195 ข. 245
ค. 205 ง. 225
ตอบ ข. 245 เป็นอนุกรมสะสมทีละ 3 ตัว
วิธีคิด
![]()
![]()
![]()
![]() 15 25 35 75 135 (245)
15 25 35 75 135 (245)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
9. ถ้า 2 * 4 = 14
และ 3 * 5 = 23
แล้ว 4 * 6 = ?
ก. 34 ข. 36
ค. 38 ง. 40
ตอบ ก. 34
แนวคิด 2 x 4 + 6 = 14 3 x 5 + 8 = 23 4 x 6 + 10 = (34)
10. ถ้า 6 * 2 = 38
และ 4 * 7 = 23
แล้ว 5 * 1 = ?
ก. 26 ข. 27
ค. 31 ง. 35
ตอบ ก. 26
แนวคิด 62 + 2 = 38 42 + 7 = 23 52 + 1 = (26)
11. 8 37 66 19 …..
ก. 4 ข. 6
ค. 9 ง. 20
ตอบ ก. 4 เป็นอนุกรมแบบผลต่างยกกำลัง
![]()
![]()
![]()
![]()
![]() วิธีคิด 8 37 66 19 (4)
วิธีคิด 8 37 66 19 (4)
81 +0 62 +1 43 +2 24 +3 05 +4
12. 2 4 8 10 20 22 …..
ก. 24 ข. 48
ค. 40 ง. 44
ตอบ ง. 44 เป็นอนุกรมแบบเป็นชุด
วิธีคิด 2 4 8 10 20 22 (44)
+2 x2 +2 x2 +2 x2
13. ถังใบหนึ่งบรรจุน้ำเต็มถึง รั่วไป 1/3 ถัง และตักออก
ก.
ค.
ตอบ ง.
แนวคิด ให้ถังจุน้ำทั้งหมด = 1
รั่วและตักออก = \
+ 4 =
\ -
= 4 \
= 4
\ 1 ส่วน = 4 x 6 = 24
ดังนั้น ถังจุน้ำได้ 24 ลิตร
14. แอลกอฮอล์ 50%
เข้มข้นกี่เปอร์เซ็นต์
ก. 25% ข. 30%
ค. 35% ง. 40%
ตอบ ค. 35%
แนวคิด แอลกอฮอล์ 50%
แอลกอฮอล์ 30%
แอลกอฮอล์
แอลกอฮอล์ = 35%
15. เลขจำนวน 2 จำนวน ห.ร.ม. = 4 และ ค.ร.น. = 360 ถ้าเลขจำนวนหนึ่งคือ 20 อีกจำนวนหนึ่ง
เท่ากับเท่าไร
ก. 24 ข. 40 ค. 68 ง. 72
ตอบ ง. 72
แนวคิด
|
![]() เลขจำนวนแรก
เลขจำนวนแรก
= = 72
16. อายุของทหาร ตำรวจ และพลเรือน 3 คน รวมกันแล้วเฉลี่ยเท่ากับ 25 ปี ถ้าอายุทั้ง 3 คนไม่มีใคร
อายุต่ำกว่า 20 ปี อยากทราบว่าคนที่มีอายุมากที่สุดจะมีอายุเท่าไร
ก. 30 ปี ข. 35 ปี
ค. 38 ปี ง. 40 ปี
ตอบ ข. 35 ปี
แนวคิด อายุ 3 คน = 3 x 25 = 75 ปี
อายุน้อยที่สุด = 20 + 20 = 40 ปี
ดังนั้น = 75 – 40 = (35 ปี)
17. กางเกงตัวหนึ่งติดราคาไว้ 80 บาท ต่อมาได้ประกาศลดราคาลง 20% นายมีเป็นลูกค้าประจำจึงลด
ให้เขาเป็นพิเศษอีก 10% ดังนั้น นายมี จะซื้อกางเกงตัวนี้ได้ในราคาเท่าใด
ก. 55 บาท ข. 57 บาท
ค. 57.60 บาท ง. 65.70 บาท
ตอบ ค. 57.60 บาท
แนวคิด ปิดราคา 100 บาท ขาย 80 บาท
ดังนั้น ปิดราคา 80 บาท ขายไป 80 x = 64 บาท
และลด 10% จะได้ 90 x = (57.60) บาท
พิจารณารูปแล้วตอบคำถามข้อ 18. – 22.
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
22 23 24 25 26 27 28 29 30
18. ถ้าอัตราการเพิ่มของนักเรียนชายเป็นไปตามปี 2527 – 2530 เราคาดไว้ว่าในปี 2531 จะมีนักเรียนชายกี่คน
ก. 200 คน ข. 250 คน
ค. 300 คน ง. 350 คน
ตอบ ค. 300 คน
วิธีคิด ตั้งแต่ปี 2527 นักเรียนชายเพิ่มขึ้นในอัตราส่วนคงที่ คือ ปีละ 50 คน ดังนั้น ปี 2531 จะมี 300 คน
19. ปี พ.ศ. ใดที่นักเรียนชายมีจำนวนเท่ากับนักเรียนหญิง
ก. 2523 ข. 2524
ค. 2525 ง. 2527
ตอบ ง. 2527
วิธีคิด ปี 2527 มีนักเรียนชายเท่ากับนักเรียนหญิง คือ จำนวน 100 คน
20. ถ้าทางโรงเรียนเก็บค่าเล่าเรียนจากนักเรียนเท่ากันทุกคน ปีใดจะเก็บเงินได้น้อยที่สุด
ก. 2521 ข. 2522
ค. 2523 ง. 2524
ตอบ ข. 2522
วิธีคิด ปี 2522 จะเก็บเงินได้น้อยที่สุด เพราะมีนักเรียนชาย-หญิงรวมกันได้ 50 + 50 เท่ากับ 100 คนเท่านั้น
21. ปีใดที่นักเรียนชายมีจำนวนมากที่สุด
ก. 2530 ข. 2529
ค. 2528 ง. 2527
ตอบ ก. 2530
วิธีคิด ปี 2530 จะมีจำนวนนักเรียนชายทั้งสิ้น 250 คน
22. ปีที่นักเรียนชายมีจำนวนเท่ากับนักเรียนหญิงมีจำนวนนักเรียนเท่าใด
ก. 200 คน ข. 150 คน
ค. 250 คน ง. 100 คน
ตอบ ง. 100 คน
วิธีคิด ปี 2527 มีนักเรียนชาย-หญิง อย่างละ 100 คน
แบบทดสอบวัดความเข้าใจโจทย์ปัญหาทางคณิตศาสตร์
23. ข้อใดมีค่ามากที่สุด
ก. a + 1 ข. a-1
ค. a 1 ง. a x 1
ตอบ ก. a + 1
สมมติว่า a เป็นจำนวนเต็ม
ก. a + 1 = 1 + 1 = 2 ข. a-1 = 1-1 = 0
ค. a 1 =
= 1 ง. a
1 = 1
1 =1
จำนวนที่มีค่ามากที่สุดคือ 1 + 1 = 2
24. ค่าเฉลี่ยของคะแนน 25, 27, 38 , 41 และ 50 ได้แก่ข้อใด
ก. 41.2 ข. 41.3
ค. 41.4 ง. 36.2
ตอบ ง. 36.2
สมมติว่า a เป็นจำนวนเต็ม
เฉลี่ย = ผลรวมของข้อมูลคะแนนทั้งหมดโดยใช้สูตร N = จำนวนข้อมูล
แทนค่า x = = 36.2
25. a2 . a5 มีค่าเท่าไร
ก. a3 ข. 2a7
ค. a7 ง. a10
ตอบ ค. a7
การหาผลคูณของเลขยกกำลังเมื่อมีฐานเดียวกันหรือฐานเท่ากันในที่นี้คือฐาน a) หาได้
โดยเอาตัวเลขยกกำลังมารวมกัน a2 a5 = a 2+5 = a7
26. มีทีมฟุตบอลสมัครเล่นร่วมแข่งขัน 10 ทีม ถ้าจัดการแข่งขันแบบพบกันหมดในรอบแรกจะต้อง
จัดแข่งขันทั้งหมดกี่ครั้ง
ก. 45 ข. 40
ค. 50 ง. 35
ตอบ ก. 45
ทีมฟุตบอลทีมหนึ่งๆ จะต้องพบกับทีมอื่นๆ 9 ครั้ง
ทีมฟุตบอลทั้งหมด 10 ทีม จะพบกัน 9 10 = 90 ครั้ง
หักจำนวนครั้งที่ซ้ำกันออกครึ่งหนึ่ง เช่น การพบกันระหว่าง A กับ B ซ้ำกับ B กับ A จะได้จำนวนการแข่งขันจริงทั้งหมด = 45 ครั้ง
27. แดงมีเงินเป็น 2 เท่า ของดำ ดำมีเงินเป็น ของเขียว เขียวมีเงิน 200 บาท แดงมีเงินเท่าไร
ก. 150 ข. 200
ค. 300 ง. 500
ตอบ ค. 300
จากโจทย์ เขียวมีเงิน 200 บาท
โจทย์ประเภทนี้ใช้วิธีคำนวณจากท้ายมาหาคำตอบ ดังนี้
ถ้าดำมีเงิน ของเขียว คือ
200 = 150 บาท แสดงว่าดำมีเงิน 150 บาท
แดงมีเงิน 2 เท่าของดำ คือ 2 150 = 300 บาท แสดงว่าแดงมีเงิน 300 บาท

 28. จงหาพื้นที่แรเงา หากสี่เหลี่ยมยาวด้านละ 14 นิ้ว
28. จงหาพื้นที่แรเงา หากสี่เหลี่ยมยาวด้านละ 14 นิ้ว
ก. 154 ตร.นิ้ว ข. 42 ตร.นิ้ว
ค. 174 ตร. นิ้ว ง. 157 ตร.นิ้ว
ตอบ ข. 42 ตร.นิ้ว
พื้นที่สี่เหลี่ยมจัตุรัส = 14 14 = 196 ตารางนิ้ว
พื้นที่วงกลม = =
7
7 = 154 ตารางนิ้ว
พื้นที่แรเงา = 196 – 154 = 42 ตารางนิ้ว
![]()
![]()
 29. ส่วนที่แรเงาคิดเป็นกี่องศา
29. ส่วนที่แรเงาคิดเป็นกี่องศา
ก. 145o ข. 104o
ค. 160o ง. 126o
ตอบ ง. 126o
พื้นที่ 100% มีค่า = 360 องศา ( เต็มรูปวงกลม = 360o)
พื้นที่ 35% มีค่า = 126 องศา
30. 8 มากกว่า
เท่าไร
ก. 8 ข. 7
ค. 7 ง. 7
ตอบ ง. 7
คำนวณโดยวิธีลบ คือ (8 -
= 8-1
= 7
32. นายขาวมีเงิน 32 บาท ถ้าให้แดงเสีย 4 บาท แดงจะมีเงินครึ่งหนึ่งของขาว เดิมแดงมีเงินกี่บาท
ก. 14 บาท ข. 6 บาท
ค. 8 บาท ง. 10 บาท
ตอบ ง. 10 บาท
สมมุติให้แดงมีเงิน 4 บาท
จะได้สมการ = x + 4 =
x + 4 =
x + 4 = 14
x = 14 – 4
x = 10
33. รัศมีของวงกลมเพิ่มขึ้น 100% พื้นที่ของวงกลมจะเพิ่มขึ้นเท่าไร
ก. 2 เท่า ข. 6 เท่า
ค. 4 เท่า ง. 6 เท่า
ตอบ ค. 4 เท่า
สมมุติให้เดิมรัศมีของวงกลมยาว = 1 นิ้ว
รัศมีเพิ่มขึ้น 100% จะเป็น = 1+1 = 2 นิ้ว
พื้นที่วงกลมเดิม =
พื้นที่วงกลมใหม่ =
พื้นที่ของวงกลมเพิ่มขึ้น = 4 เท่า
34. ปักเสาโทรเลขห่างกันด้านละ 25 เมตร ระยะทางห่างกัน 500 เมตร จะต้องใช้เสากี่ต้น
ก. 12 ข. 20
ค. 21 ง. 22
ตอบ ค. 21
ต้องใช้เสาโทรเลข ต้น
![]() (สูตรการคำนวณแบบนี้ต้องใช้สูตร ระยะทาง + 1 )
(สูตรการคำนวณแบบนี้ต้องใช้สูตร ระยะทาง + 1 )
ระยะห่าง
35. มีไก่และหมูอยู่ในบ้านเดียวกันรวม 12 ตัว
ก. 1 ข. 2
ค. 3 ง. 4
ตอบ ค. 3
สมมติมีหมู x ตัว มีขา x ขา ( หมู 1 ตัว มี 4 ขา)
มีไก่ 12-x ตัว จึงมีขา (2 (12-x) ขา (ไก่ 1 ตัว มี 2 ขา)
โจทย์บอกว่า ขาของไก่มีมากกว่าขาของหมู 6 ขา
2 (12-x) – 4x = 6
24 – 2x – 4x = 6
6x = 18
X = 3 มีหมู 3 ตัว
36. ขณะนี้ ศักดิ์มีอายุเป็น 3 เท่าของลูก เมื่อ 10 ปีที่แล้ว อายุของลูกเป็น 1 ใน 7 เท่าของพ่อ ขณะนี้
ลูกมีอายุ
ก. 10 ข. 15
ค. 20 ง. 25
ตอบ ข. 15
โจทย์แบบนี้ต้องสมมุตว่าต้องการทราบเป็น x
สมมุติอายุปัจจุบันของลูก = x ปี พ่อมีอายุ 3x ปี
เมื่อ 10 ปีที่แล้ว ลูกมีอายุ = x – 10
เมื่อ 10 ปีที่แล้ว พ่อมีอายุ = 3x – 10
โจทย์บอกว่าเมื่อสิบปีที่แล้วอายุของลูกเป็น ของพ่อ
จะได้สมการดังนี้ x - 10 = (3x – 10)
7x – 70 = 3x – 10
7x – 3x = 70 – 10 -60
4x = 60 , x = = 15
37. 2 ลูกบาศก์หลา เท่ากับกี่ลูกบาศก์ฟุต
ก. 6 ค. 18
ข. 27 ง. 54
ตอบ ง. 54
1 หลา = 3 ฟุต
1 ลูกบาศก์หลา = 3 3
3 ลูกบาศก์ฟุต
2 ลูกบาศก์หลา = 23
3
3 = 54 ลูกบาศก์ฟุต
38. เลข 3 จำนวนเรียงกัน ผลบวกของเลขจำนวนน้อย กับจำนวนมากเท่ากับ 108 จงหาผลรวม
เลข 3 จำนวนนั้น
ก. 121 ข. 53
ค. 155 ง. 162
ตอบ ง. 162
สมมติว่าเลขจำนวนแรกคือ x จำนวนถัดไปคือ x + 1 , x+2
( เลขเรียงผลรวมของเลขจำนวนน้อย (x) กับเลขจำนวนมาก (x+2)
จะได้ x + (x+2) = 108
เมื่อ x + (x + 2) = 108
2x +2 = 108
2x = 108 - 2
x =
ดังนั้น เลขสามจำนวนเรียงกัน คือ 53 + 54 + 55 = 162
39.โดนัทชิ้นละ 12 บาท ซื้อ 5 ชิ้น + เงิน 1 บาท ได้ฟรี 1 ชิ้น นักเรียน 38 คน แจกคนละชิ้น ต้องจ่ายเงิน
เท่าไร
ก. 390 บาท ค. 360
ข. 366 บาท ง. 420
ตอบ ก. 390 บาท
วิธีคิด ซื้อ 5 ชิ้น + เงิน 1 บาท ได้ฟรี 1 ชิ้น
ถ้า ซื้อ 10 ชิ้น + เงิน 2 บาท ได้ฟรี 2 ชิ้น
ถ้า ซื้อ 15 ชิ้น + เงิน 3 บาท ได้ฟรี 3 ชิ้น
ถ้า ซื้อ 20 ชิ้น + เงิน 4 บาท ได้ฟรี 4 ชิ้น
ถ้า ซื้อ 25 ชิ้น + เงิน 5 บาท ได้ฟรี 5 ชิ้น
ถ้า ซื้อ 30 ชิ้น + เงิน 6 บาท ได้ฟรี 6 ชิ้น
เลือกซื้อ 30 ชิ้น + ฟรี 6 ชิ้น = 36 ชิ้น และต้องซื้อเพิ่มอีก 2 ชิ้น จึงจะครบ 38 ชิ้น
โดนัท ชิ้นละ 12 จะต้องจ่ายเงิน 32*12+6 = 390 บาท
*****ดังนั้น ต้องจ่ายเงิน 390 บาท จึงจะได้ครบ 38 คน คนละชิ้น
40. ข้อใดมีค่าน้อยที่สุด
ก. 2% ของ 400 ข. 3% ของ 350
ค. 4% ของ 300 ง. 5% ของ 250
ตอบ ก. 2% ของ 400
คำนวณหาค่า
ก. 2% ของ 400 = 8 ข. 3% ของ 350 = 10.5
ค. 5% ของ 230 = 11.5 ง. 4% ของ 300 = 12
41. สี่เหลี่ยมจัตุรัสมีพื้นที่ 49 จะมีเส้นรอบรูปยาวเท่าไร
ก. 7 ข. 14
ค. 21 ง. 28
ตอบ ง. 28
พื้นที่สี่เหลี่ยมจัตุรัส =
ด้านหนึ่งของรูปสี่เหลี่ยมจัตุรัส = (ถาดรากกำลังสอง)
เส้นรอบรูปยาว 4 =
42. ร้านค้าคิดราคาขายสินค้าไว้สูงกว่าต้นทุนหนึ่งเท่าตัว และประกาศขายลดราคาให้แก่ผู้ซื้อ 40%
เขายังมีกำไรอีกร้อยละเท่าไร
ก. 15 ข. 20
ค. 25 ง. 30
ตอบ ข. 20
ปิดราคาขายไว้สูงเท่าตัว หมายความว่า ราคาจริง 100 ปิดราคาขายไว้ 200 บาท
ประกาศขายลดราคา 40% หมายความว่า ปิดราคา 100 ขายเพียง 100 – 40 = 60 บาท
ปิดราคาไว้ 200 ขายจริงเพียง 120 บาท แต่ต้นทุนจริงเพียง 100 บาท
แสดงว่า ต้นทุนจริง 100 บาท ยังได้กำไร 120 – 100 = 20 บาท
43. 30% ของ 27 มีค่าเท่าไร
ก. น้อยกว่า 100 อยู่ 9 ข. มากกว่า 100 อยู่ 9
ค. น้อยกว่า 100 อยู่ 19 ง. มากกว่า 100 อยู่ 19
ตอบ ค. น้อยกว่า 100 อยู่ 19
30% หมายความว่า ในจำนวนเต็ม 100 มีค่า 30
ในจำนวนเต็ม 270 มีค่า =81
ข้อ ค ถูก เพราะว่าน้อยกว่า 100 อยู่ 19 คือ 100 – 19 = 81
44. ห้องเรียนห้องหนึ่งมีเด็ก 15 คน ในวันปีใหม่ต่างคนต่างส่งของขวัญให้แก่กันและกันคนละ 1 ชิ้น
จะมีทั้งหมดกี่ชิ้น
ก. 210 ข. 205
ค. 215 ง. 220
ตอบ ก. 210
นักเรียนทั้งหมด 15 คน นักเรียนคนหนึ่งๆ ต้องส่งของขวัญให้เพื่อน = 14 ชิ้น
(หักตัวเองออก) จะมีของขวัญทั้งหมด 15 14 = 210 ชิ้น
45. นาฬิกาเรือนหนึ่งเมื่อครบ 30 นาที จะตีหนึ่ง เมื่อครบชั่วโมงจะตีจำนวนครั้งเท่าตัวเลขที่เข็มสั้น
ชี้อยู่ อยากทราบว่าตั้งแต่เวลา 8.15 น. จนถึง 12.04 น. นาฬิกาเรือนนี้จะตีกี่ครั้ง
ก. 30 ข. 42
ค. 46 ง. 50
ตอบ ค. 46
เมื่อครบ 30 นาทีตี 1 ครั้ง มีเวลา 8.30 , 9.30, 10.30, 11.30 = 4 ครั้ง เมื่อครบ 1 ชั่วโมง
ตีตามจำนวนชั่วโมง คือ 9+10+11+12 = 42 ครั้ง จำนวนครั้งที่ตี 4 + 42 = 46 ครั้ง
46. ผลบวกของเลข 2 จำนวนเท่ากับ 140 ผลต่างกันเท่ากับ 20 เลขทั้งสองจำนวนนี้คืออะไร
ก. 30 , 60 ข. 60 , 80
ค. 80 , 100 ง. 90 , 100
ตอบ ข. 60 , 80
สมมติเลข 2 จำนวนนี้ = x และ y
จะได้สมการ x + y = 140 ……..(1)
x- y = 120 …… (2)
นำ (1) + (2) จะได้ 2x = 160, x =
นำ (1) – (2) จะได้ 2y = 120 , y =
47. 25 เป็นกี่เท่าของผลบวก 9.5 กับ 10.5
ก. เท่า ข.
เท่า
ค. เท่า ง.
เท่า
ตอบ ค. เท่า
คำนวณหาค่าแล้วเปรียบเทียบ คือ 9.5 + 10.5 = 20
2.5 เป็นกี่เท่าของ 20 คือ เท่า
48. ห้องขนาด 5 6
5 เมตร ถ้าวัดโดยรอบจะมีความยาวกี่เมตร
ก. 11 เมตร ข. 16 เมตร
ค. 20 เมตร ง. 22 เมตร
ตอบ ง. 22 เมตร ห้องมีขนาด 56
5 เมตร หมายความว่า กว้าง
ยาว
สูง
นั่นคือ ห้องกว้าง 5 เมตร 2 ด้าน และยาว 6 เมตร (2 ด้าน)
ถ้าวัดโดยรอบจะยาว = (52 + 6
2) = 10 + 12 = 22 เมตร
49. ม้า วัว และไก่ นับขารวมกันได้ 200 ขา ทั้งสามชนิดมีจำนวนตัวเท่ากัน อยากทราบว่ามีสัตว์
อย่างละกี่ตัว
ก. 14 ตัว ข. 16 ตัว
ค. 18 ตัว ง. 20 ตัว
ตอบ ง. 20 ตัว
ม้า วัว และไก่ อย่างละ 1 ตัว นับขารวมกันได้ = 10 ขา (4+4+2)
นับขารวมกันได้ 10 ขา มี ม้า วัว และไก่ อย่างละ 1 ตัว
ถ้า “ 200 ” ตัว
51. เลขคู่จำนวนบวก 2 จำนวนเรียงกัน คูณกันได้ผลลัพธ์เท่ากับ 360 เลขคู่จำนวนถัดไปมีค่าเท่าไร
ก. 18 ข. 20
ค. 22 ง. 24
ตอบ ค. 22
ให้เลขคู่ 2 จำนวน เรียงกันนั้น คือ x และ x+2
x (x+2) = 360
x2 + 2x = 360
x2 +2x-360 = 0 , (x+20)(x-18) = 0, x=18, 20
เลขคู่ 2 จำนวนนั้นคือ 18 กับ 20 จำนวนถัดไปจึงได้แก่ 22
ข้อ 52-55 พิจารณาว่าจำนวนใดเมื่อนำมาแทนใน ¨ แล้วได้อนุกรมที่ถูกต้อง
52. 51 44 ¨ 33 29 ¨
ก. 47,22 ข. 39,20
ค. 38,26 ง. 53,21
ตอบ ค. 38,26
วิธีคิด 51 - 7 = 44
![]() ( 44 - 7 ) + 1 = 38
( 44 - 7 ) + 1 = 38
( 38 - 7 ) + 2 = 33
![]() ( 33 - 7 ) + 3 = 29
( 33 - 7 ) + 3 = 29
( 29 - 7 ) + 4 = 26
53. 48 ¨ 44 41 ¨ 37 34 ¨ 30
ก. 46,39,32 ข. 45,39,30
ค. 46,38,92 ง. 47,38,30
ตอบ ก. 46,39,32
![]() วิธีคิด 48 – 2 = 46
วิธีคิด 48 – 2 = 46
46 – 2 = 44
44 - 3 = 41
![]() 41 - 2 = 39
41 - 2 = 39
39 - 2 = 37
37 - 3 = 34
![]() 34 - 2 = 32
34 - 2 = 32
32 - 2 = 30
54. 121 11 100 10 81 ¨
ก. 9 ข. 11
ค. 13 ง. 15
ตอบ ก. 9
121 ถอดรากที่สองได้ 11
100 ถอดรากที่สองได้ 10
81 ถอดรากที่สองได้ 9
56. จากข้อความที่กำหนดให้ตัวเลือกข้อใดถูกต้อง
¶ มีค่าเป็น 13 เท่าของ 2
¯ มีค่าเป็น เท่าของ 14
|
คอลัมน์ ก |
คอลัมน์ ข |
|
¯ + ( 2 x ¶) |
( ¯ + ¶ ) x 2 |
ก. ผลลัพธ์ในคอลัมน์ ก มีค่ามากกว่าคอลัมน์ ข
ข. ผลลัพธ์ของทั้งสองคอลัมน์เท่ากัน
ค. ผลลัพธ์ในคอลัมน์ ข มีค่ามากกว่าคอลัมน์ ก
ง. ข้อมูลที่ให้ไม่เพียงพอต่อการเปรียบเทียบ
ตอบ ค. ผลลัพธ์ในคอลัมน์ ข มีค่ามากกว่าคอลัมน์ ก
¶ มีค่าเป็น 13 เท่าของ 2
คือ 13 x 2 = 26
¯ มีค่าเป็น เท่าของ 14
คือ x 14 = 147
คอลัมน์ ก ¯ + ( 2 x ¶) = 147 + ( 26 x 2 ) = 199
คอลัมน์ ข ( ¯ + ¶ ) x 2 = (147 + 26 ) x 2 = 346
ดังนั้น ผลลัพธ์ในคอลัมน์ ข มีค่ามากกว่าคอลัมน์ ก
57. เมื่อนำ 2 ไปลบจาก a จะมีค่าเท่ากับ 7 และถ้านำ 2 ไปบวกกับ b จะมีค่าเท่ากับ a จง หาว่า a
มีค่าเท่าใด
ก. 5 ข. 9
ค. 11 ง. 15
ตอบ ข. 9
a - 2 = 7
a = 9
b + 2 = 9
b = 7
58. ติ๊กอายุมากกว่าเต๋า 5 ปี เต๋าแก่กว่าว่านัท 3 ปี นัทอายุอ่อนกว่าแอน 2 ปี และติ๊กอายุอ่อนกว่าอู๋
1 ปี ถ้านัทอายุ 38 ปี ติ๊กจะมีอายุเท่าใด
ก. 42 ข. 48
ค. 46 ง. 45
ตอบ ค. 46
สมมุติให้ติ๊กอายุ x ปี
สมมุติให้เต๋าอายุ y ปี
สมมุติให้นัทอายุ z ปี
ติ๊กอายุมากกว่าเต๋า 5 ปี ติ๊กอายุ x ปี ดังนั้น x = y + 5
เต๋าแก่กว่านัท 3 ปี เต๋าอายุ y ปี ดังนั้น y = z + 3
จากโจทย์กำหนดให้นัทอายุ 38 ปี
ดังนั้น y = 38 + 3
y = 41 ปี
แทนค่า y ในสมการที่ 1
x = y + 5
x = 41 + 5 = 46
ถ้านัทอายุ 38 ปี ติ๊กจะมีอายุ 46 ปี
59. เลขสองจำนวนเมื่อบวกกันได้ผลบวกเป็น 108 ถ้าจำนวนหนึ่งเท่ากับ 52 ผลคูณของสองจำนวน
นั้นเป็นเท่าใด
ก. 2,912 ข. 2,913
ค. 3,085 ง. 3,086
ตอบ ก. 2,912
x + y = 108
ให้ x เท่ากับ 52
52 + y = 108
y = 108 - 52 = 56
ผลคูณของทั้งสองจำนวน คือ 52 x 56 = 2,912
60. เมื่อ 10 ปีแล้ว น้อยอายุ x ปี อีก a ปี น้อยจะอายุเท่าใด
ก. ( x – 10 ) + a ปี ข. x – 12 - a ปี
ค. ( 10 – x ) + a ปี ง. ( x +10 ) + a ปี
ตอบ ง. ( x +10 ) + a ปี
“เมื่อ 10 ปีที่แล้ว น้อยอายุ x ปี”
ปัจจุบัน น้อยมีอายุ = x + 10 ปี
อีก a ปี น้อยจะอายุ = อายุปัจจุบัน + a
= ( x + 10) + a ปี
61. ตุ๊กตามีซาลาเปาซึ่งเป็นรูปวงกลมอยู่ 2 ลูก ถ้าแบ่งแต่ละลูกออกเป็น 4 ชิ้น เท่าๆกันโดยยึด
จุดศูนย์กลางเป็นหลัก ผลรวมของซาลาเปาทั้งสองชิ้นจะทำมุมกี่องศา
ก. 45o ข. 90o
ค. 180o ง. 360o
ตอบ ค. 180o
วงกลมหนึ่งวง 360o
แบ่งออกเป็น 4 ชิ้นเท่าๆกัน = 90 o
ผลรวมของซาลาเปาทั้งสองชิ้นทำมุม 90o + 90 o = 180o
62. ถ้า A เป็น ห.ร.ม. ของ 12, 8
B เป็น ห.ร.ม. ของ 16, 24 ข้อใดสรุปถูกต้อง
|
คอลัมน์ ก |
คอลัมน์ ข |
|
|
|
ก. ผลลัพธ์ของคอลัมน์ ก มากกว่าคอลัมน์ ข
ข. ผลลัพธ์ของคอลัมน์ ข มากกว่าคอลัมน์ ก
ค. ผลลัพธ์ของคอลัมน์ ก และ ข มีค่าเท่ากัน
ง. ข้อมูลที่ให้ไม่เพียงพอต่อการเปรียบเทียบ
ตอบ ข. ผลลัพธ์ของคอลัมน์ ข มากกว่าคอลัมน์ ก
A เป็น ห.ร.ม. ของ 12, 8 A = 4
B เป็น ห.ร.ม. ของ 16, 24 B = 8
คอลัมน์ ก x 2 =
x 2 = 1
คอลัมน์ ข + 2 =
2 = 4
ดังนั้น ผลลัพธ์ของคอลัมน์ ข มากกว่าคอลัมน์ ก
63. ถ้า x มีค่าเท่ากับ 9 % ของ 300
y มีค่ามากกว่า 58 อยู่ 23
|
คอลัมน์ ก |
คอลัมน์ ข |
|
|
|
ก. ผลลัพธ์ของคอลัมน์ ก มากกว่าคอลัมน์ ข
ข. ผลลัพธ์ของคอลัมน์ ข. มากกว่าคอลัมน์ ก
ค. ผลลัพธ์ของคอลัมน์ ก และ ข มีค่าเท่ากัน
ง. ข้อมูลที่ให้ไม่เพียงพอต่อการเปรียบเทียบ
ตอบ ข. ผลลัพธ์ของคอลัมน์ ข. มากกว่าคอลัมน์ ก
ถ้า x มีค่าเท่ากับ 9% ของ 300
x = x 300 = 27
y มีค่ามากกว่า 58 อยู่ 28
y = 58 – 23
y = 81
คอลัมน์ ก ของ x =
x 27
= 13.5
คอลัมน์ ข ของ y =
x 81
= 45
จะได้ 13.5 < 45
ผลลัพธ์ของคอลัมน์ ข มากกว่าคอลัมน์ ก
64. จะมีค่ามากกว่า 2 เมื่อใด เมื่อ c เป็นจำนวนนับ
ก. เมื่อ c น้อยกว่า 3 ข. เมื่อ c มากกว่า 3
ค. เมื่อ c เท่ากับ 3 ง. ไม่มีคำตอบที่ถูกต้อง
ตอบ ก. เมื่อ c น้อยกว่า 3
เมื่อ c เป็นจำนวนนับ จะมีค่ามากกว่า 2 เมื่อ c น้อยกว่า 3
เช่น = 6
65. ในงานเลี้ยงสังสรรค์แห่งหนึ่ง มีผู้มาร่วมงาน 24 คน แต่ละคนจะต้องเข้าไปทักทายกันโดย
การสัมผัสมือซึ่งกันและกัน รวมแล้วจะมีการสัมผัสมือกันทั้งหมดกี่ครั้ง
ก. 270 ครั้ง ข. 272 ครั้ง
ค. 274 ครั้ง ง. 276 ครั้ง
ตอบ ง. 276 ครั้ง
แนวคิด การสัมผัสมือแต่ละครั้งประกอบด้วยคน 2 คน ดังนั้นคน 24 คนจะมีการสัมผัสกัน
กี่ครั้ง ใช้สูตรการจัดหมู่ =
เมื่อ n = จำนวนทั้งหมด = 24 คน
r = 2 (เพราะการสัมผัสมือแต่ละครั้งประกอบด้วยคน 2 คน)
และ n! = n (n-1)
(n-2)
……
1
แทนค่าในสูตรจะได้
= 23 12 = 276
ดังนั้นมีการสัมผัสมือกันในงานทั้งหมด 276 ครั้ง
66. ถ้าเพิ่มรัศมีของวงกลมขึ้นเป็น 2 เท่า ของรัศมีเดิม พื้นที่ของวงกลมใหญ่จะเพิ่มขึ้นเป็นกี่เท่าของ
พื้นที่เดิม
ก. 2 เท่า ข. 4 เท่า
ค. 6 เท่า ง. 8 เท่า
ตอบ ข. 4 เท่า
แนวคิด สมบัติรัศมีวงกลมเดิม = 1 หน่วย
เพิ่มรัศมีเป็น 2 เท่าของรัศมีเดิม
รัศมีวงกลมใหญ่ = 1
2 = 2 หน่วย
นั่นคือ พท. วงกลมเดิม =
ดังนั้น พื้นที่วงกลมใหญ่ เพิ่มขึ้นเป็น 4 เท่า ของพื้นที่วงกลมเดิม
67. ไก่และหมูจำนวนหนึ่งเมื่อนับขาไก่ปรากฏว่าเป็น 4 เท่าของขาหมู และหัวไก่มีจำนวนมากกว่า
หัวหมูอยู่ 14 หัว จงหาว่า มีไก่และหมูอย่างละกี่ตัว
ก. มีไก่ 14 ตัว หมู 4 ตัว ข. มีไก่ 16 ตัว หมู 2 ตัว
ค. มีไก่ 16 ตัว หมู 4 ตัว ง. มีไก่ 18 ตัว หมู 6 ตัว
ตอบ ข.
แนวคิด สมมติให้มีไก่ X ตัว หมู Y ตัว
ขาของไก่ทั้งหมดมี 2X ขา
ขาของหมูทั้งหมดมี 4Y ขา
จำนวนขาไก่เป็น 4 เท่าของหมู
2X = 4(4Y)
2X = 16Y
X = 8Y ……………(1)
และหัวไก่มากกว่าหัวหมู 14 หัว
X – Y = 14 …………. (2)
จาก (1) และ (2) จะได้ 8Y – Y = 14
7Y = 14
Y = 2
มีหมูทั้งหมด 2 ตัว
แทนค่า Y = 2 ใน (1) จะได้ X = 8(2) = 16
มีไก่ 16 ตัว
68. นายชูศิลป์ ซื้อน้ำหอมมา 120 ขวด ราคาขวดละ 12.50 บาท แล้วเขานำน้ำหอมไปผสมกับ
น้ำเปล่าจำนวนหนึ่งแล้วขายไปในราคาเท่าเดิม ปรากฏว่าได้กำไร 12.5 % จงหาว่าเขาผสมน้ำเปล่า
ลงไปกี่ขวด
ก. 10 ขวด ข. 15 ขวด
ค. 16 ขวด ง. 18 ขวด
ตอบ ข. 15 ขวด
แนวคิด นายชูศิลป์ซื้อน้ำหอมมาเป็นเงิน 129 12.50 บาท นำไปผสมน้ำเปล่าแล้วขายไปราคาเท่าเดิม คือ 12.50 บาท
ปรากฏว่าได้กำไร 12.5%
ทุน (ซื้อมา) 100 บาท ขายไป 100 + 12.5 = 112.5 บาท
ทุน (ซื้อมา) 120
12.50 บาท ขายไป
= 1687.50 บาท
นำไปขายราคาเดิมคือขวดละ 12.50 บาท
คิดเป็นน้ำหอมผสม 1687.50 ¸ 12.50 = 135 ขวด
ดังนั้นเขาผสมน้ำเปล่าลงไป 135 – 120 = 15 ขวด
69. เมื่อ 10 ปีที่แล้ว ดำรัสอายุ 15 ปี อีก 15 ปีข้างหน้า ดำรัสจะมีอายุเท่าไร่
ก. 30 ปี ข. 35 ปี
ค. 40 ปี ง. 45 ปี
ตอบ ค. 40 ปี
แนวคิด เมื่อ 10 ปีที่แล้ว ดำรัสอายุ 15 ปี
ดังนั้น ปัจจุบัน ดำรัสอายุ 10 + 15 = 25 ปี
อีก 15 ปีข้างหน้า ดำรัสจะมีอายุ 25 + 15 = 40 ปี
70. เลข 2 จำนวนมีผลบวกเท่ากับ 40 และผลต่างเท่ากับ 8 จงหาเลขจำนวนน้อย
ก. 12 ข. 14
ค. 16 ง. 18
ตอบ ค. 16
แนวคิด ให้เลขจำนวนน้อยเป็น X
เลขจำนวนมากเป็น X + 8
และ X + ( X + 8 ) = 40
2X = 40 - 8
2X = 32
X = 32 ¸ 2
x = 16
ดังนั้น เลขจำนวนน้อย คือ 16 (จำนวนมากคือ 40 – 16 = 24 )
71. แขกที่มาในงานเลี้ยงแห่งหนึ่งมี 20 คน แต่ละคนจะต้องแลกของขวัญซึ่งกันและกันให้ครบทุกคน
จงหาจำนวนของขวัญทั้งหมดว่ามีกี่ชิ้น
ก. 360 ชิ้น ข. 380 ชิ้น
ค. 390 ชิ้น ง. 400 ชิ้น
ตอบ ข. 380 ชิ้น
แนวคิด แขกที่มาในงานทั้งหมดมี 20 คน แขกแต่ละคนจะต้องเตรียมของขวัญมาให้แก่คนอื่น
(ยกเว้นตนเอง) จำนวน 20 – 1 = 19 ชิ้น
แขกจำนวน 20 คน จะมีของขวัญทั้งหมด 20
19 = 380 ชิ้น
72. ขณะนี้ลงมีอายุเป็น 3 เท่าของหลาน เมื่อ 10 ปีที่แล้ว อายุของหลานเป็น ของลุง ขณะนี้
หลานอายุเท่าใด
ก. 10 ปี ข. 15 ปี
ค. 18 ปี ง. 20 ปี
ตอบ ข. 15 ปี
แนวคิด สมมติขณะนี้หลายอายุ X ปี ลุงมีอายุเป็น 3 เท่าของหลาน
ลุงอายุ 3
X = 3X ปี
เมื่อ 10 ปีที่แล้วอายุของหลานเป็น (X-10) ปี และเมื่อ 10 ปีที่แล้วลุงอายุเป็น (3X – 10)
เมื่อ 10 ปีที่แล้วหลานมีอายุ เป็น ของลุง
จะได้สมการดังนี้
(X – 10) = (3X – 10)
X-10 = X -
X - X = 10 -
=
7X – 3X = 70 - 10
4X = 60
X =
= 15
ดังนั้น ขณะนี้หลานมีอายุ 15 ปี
แบบทดสอบ (ร้อยละหรือเปอร์เซ็นต์)
73. 2% ของจำนวนหนึ่งมีค่า 270 จำนวนนั้นมีค่าเท่าไร
ก. 1359 ข. 2700
ค. 3400 ง. 13500
ตอบ ง. 13500
แนวคิด = 13500
หรือ 2 ส่วน = 270
100 ส่วน =
74. 5% ของ 270 กับ 10% ของ 91 ต่างกันอยู่เท่าไร
ก. 4.4 ข. 5.0
ค. 9.1 ง. 13.5
ตอบ ก. 4.4
แนวคิด 5% ของ 270 =
10% ของ 91 =
ผลต่าง = 13.5 – 9.1 = 4.4
75. ข้อใดมีค่าน้อยที่สุด
ก. 3% ของ 500 ข. 4% ของ 450
ค. 5% ของ 300 ง. 6% ของ 200
ตอบ ง. 6% ของ 200
แนวคิด 3% ของ 500 =
4% ของ 450 =
5% ของ 300 =
6% ของ 200 =
76. พื้นที่วงกลมเพิ่มขึ้น 4 เท่า รัศมีเพิ่มขึ้นกี่เปอร์เซ็นต์
ก. 50% ข. 100%
ค. 200% ง. 400%
ตอบ ข. 100%
แนวคิด รัศมีเดิม r พื้นที่เดิม
พื้นที่เพิ่มขึ้น 4 เท่า = 4 =
รัศมี เพิ่มขึ้นจาก r เป็น 2r
นั่นคือ รัศมีเพิ่มขึ้น 100%
77. ติดราคาสินค้าไว้สูงกว่าทุน 1 เท่าตัว แต่ลดให้ผู้ซื้อเงินสด 30% จากราคาป้าย เขาจะได้กำไร
ร้อยละเท่าไร
ก. 30% ข. 40%
ค. 60% ง. 70%
ตอบ ข. 40%
แนวคิด ทุน 100 ติดราคาไว้ 200
ลดให้ 30% จากป้าย =
จะขายไป 140
นั่นคือได้กำไร 140-100 = 40%
78. สี่เหลี่ยมจัตุรัสด้านยาวเพิ่มขึ้น 10% พื้นที่จะเพิ่มขึ้นเท่าไร
ก. 11% ข. 20%
ค. 21% ง. 40%
ตอบ ค. 21%
แนวคิด ด้านยาว 100 พ.ท. = 10,000 ตร.หน่วย
ด้านยาว 110 พ.ท. = 12,100 ตร.หน่วย
พ.ท. เพิ่มขึ้น 2100 จาก 10,000 ตร.หน่วย
นั่นคือ เพิ่มขึ้น
79. เลข 2 จำนวนรวมกันเป็น 25 ถ้าจำนวนน้อยเป็น 40% ของ 25 จำนวนมีค่าเท่าไร
ก. 10 ข. 15
ค. 20 ง. 25
ตอบ ข. 15
แนวคิด 40% ของ 25 =
จำนวนมาก = 25 – 10 = 15
80. 15 จะมีค่าเป็น 75% ของเลขจำนวนใด
ก. 20 ข. 25
ค. 30 ง. 35
ตอบ ก. 20
แนวคิด มีค่า 15
1 มีค่า
81. 40% ของ 80% ของ 1500 มีค่าเท่าไร
ก. 400 ข. 480
ค. 520 ง. 1200
ตอบ ข. 480
แนวคิด 80% ของ 1500 =
40% ของ 1200 =
82. 20% ของผู้ชายเท่ากับ 25% ของผู้หญิง ถ้ามีคนทั้งหมด 90 คน จะมีผู้ชายมากกว่าผู้หญิงกี่คน
ก. 5 ข. 10
ค. 15 ง. 20
ตอบ ข. 10
แนวคิด X คือผู้ชาย Y คือผู้หญิง X+Y = 90 …………..(1)
=
=
…………….(2)
X =
…………(3)
เอา X จาก 3 แทนใน (1) = 90
= 90
Y =
X = 90 - 40 = 50
นั่นคือ ผู้ชายมากกว่าผู้หญิง = 50 – 40 = 10 คน
83. คน 15 คน ทำงานชิ้นหนึ่งเสร็จในเวลา 20 วัน ถ้ามีคนเพียง 10 คน จะทำงานให้เสร็จต้อง
เพิ่มเวลาอีกกี่เปอร์เซ็นต์
ก. 20% ข. 25%
ค. 50% ง. 75%
ตอบ ค. 50%
แนวคิด คน 15 คน ทำงานเสร็จ 20 วัน
คน 10 คน ทำงานเสร็จ
เวลาที่เพิ่มขึ้น 30 – 20 = 10 วัน
เพิ่มจากเวลาเดิม
84. ติดป้ายราคาสินค้าให้ได้กำไร 25% แต่จะลดให้กับผู้ซื้อเงินสด 20% จากราคาป้าย ขายสินค้าชิ้นนี้
ได้ผลอย่างไร
ก. กำไร 5% ข. กำไร 2.5%
ค. เท่าทุน ง. ขาดทุน
ตอบ ค. เท่าทุน
แนวคิด ราคาทุน 100 บาท ติดราคาไว้ 125 บาท
ลดให้ผู้ซื้อเงินสด 20% จากราคาป้าย
ราคาป้าย 100 บาท จะขายเพียง 80 บาท
ราคาป้าย 125 บาท จะขายเพียง
นั่นคือจะขายราคา 100 บาท (เท่าทุน)
85. จะเขียนเป็นร้อยละได้เท่าใด
ก. ร้อยละ 1 ข. ร้อยละ 10 ค. ร้อยละ 20 ง. ร้อยละ 40
ตอบ ค. ร้อยละ 20 ถ้า 5 ช่อง เท่าร้อยละ 100
ดังนั้น 1 ช่อง เท่ากับ = ร้อยละ 20
86. นาย ก. ได้รับเงินเดือนเพิ่มขึ้น 25% แต่เงินเดือนที่ได้รับเท่ากับเงินเดือนที่เข้าได้รับเมื่อปีก่อน
อยากทราบว่าปีที่แล้วเขาถูกลดเงินเดือนเท่าไร
ก. 10% ข. 15%
ค. 20% ง. 25%
ตอบ ค. 20%
แนวคิด ได้รับเงินเดือนเพิ่มขึ้น 25%
เดิมเงินเดือน 100 ได้รับใหม่เป็น 125
แต่เงินรับใหม่เท่ากับเงินที่ได้รับปีก่อนโน้น
นั่นคือปีก่อนโน้นได้รับเงินเดือน 125 หลังปีที่แล้วถูกลดลง 25 บาท
ปีก่อนโน้นได้รับเงินเดือน 100 หลังปีที่แล้วถูกลดลง บาท
นั่นคือปีที่แล้วเขาถูกลดเงินเดือน 20%
87. นาย ข. ได้รับเงินเดือนๆละ 5122 บาท เพราะถูกหักเข้ากองทุนประกันสังคม ถ้าอัตราเงินเดือน
ของนาย ข. คือ 5200 บาท ค่าประกันสังคมคิดเป็นกี่เปอร์เซ็นต์
ก. 0.5% ข. 0.8%
ค. 1.0% ง. 1.5%
ตอบ ง.
แนวคิด เงินเดือน 5200 บาท ได้รับจริง 5122 บาท
ถูกหักเข้ากองทุนประกันสังคม 5200 – 5122 = 78 บาท
เงินเดือน 5200 บาท ถูกหัก 78 บาท
เงินเดือน 100 บาท ถูกหัก
แบบทดสอบ (สมการและอสมการ)
88. มีไก่และหมูอยู่ในบ้านรวมกัน 12 ตัว ถ้านับขารวมกันได้ขาของไก่มากกว่าหมู 6 ขา
อยากทราบว่าในบ้านมีหมูอยู่กี่ตัว
ก. 1 ตัว ข. 2 ตัว
ค. 3 ตัว ง. 4 ตัว
ตอบ ค. 3 ตัว
แนวคิด ให้ไก่มี X ตัว มี X หัว และมี 2X ขา
หมูมี Y ตัว มี Y หัว และมี 4Y ขา
มีไก่กับหมู 12 ตัว X + Y = 12……….(1)
ขาไก่มีมากกว่าขาหมู 6 ขา 2X - 4Y = 6 ………..(2)
(2) 2
X – 2Y = 3 …………(3)
(1) - (3) 3Y = 9
Y =
มีหมูอยู่ 3 ตัว
89. ถังน้ำมันใบหนึ่งเมื่อหย่อนเชือกถึงก้นถังแล้ว ยังเหลือเชือกยาว 10 นิ้ว ถ้าทบเชือกเส้นนี้
เข้าด้วยกันแล้วหย่อนลงไปอีก ปรากฏว่ายังขาดอยู่อีก 10 นิ้ว จึงจะถึงก้นถังพอดี ถังใบนี้
สูงเท่าใด
ก. 30 นิ้ว ข. 25 นิ้ว
ค. 20 นิ้ว ง. 15 นิ้ว
ตอบ ค. 20 นิ้ว
แนวคิด ให้เชือกยาวเท่ากับ X นิ้ว
X - 10 = …………(1)
2X – 20 = X + 10
2X - X = 10+20
X = 30
เชือกยาว 30 นิ้ว และถังใบนี้สูง 30-10 = 20 นิ้ว
90. ปีนี้ ก อายุมากกว่า ข 5 ปี อีก 2 ปีข้างหน้าอายุของ ก จะเป็น 2 เท่าของอายุของ ข อยากทราบว่า
ปัจจุบัน ก มีอายุกี่ปี
ก. 6 ปี ข. 8 ปี
ค. 10 ปี ง. 12 ปี
ตอบ ข. 8 ปี
แนวคิด ให้ ก มีอายุ X ปี
ข มีอายุ = X – 5 ปี
อีก 2 ปีข้างหน้าอายุของ ก จะเป็น 2 เท่าของอายุ ข
X + 2 = 2
X + 2 = 2( X - 3)
X + 2 = 2X – 6
2X – X = 6 + 2
X = 8
ก มีอายุ 8 ปี
91. นกเอี้ยงฝูงหนึ่งบินมาเกาะหลังควาย ถ้าเกาะตัวต่อตัว จะเหลือนกเอี้ยง 1 ตัว แต่ถ้านกเอี้ยง 2 ตัว
เกาะควาย 1 ตัว จะเหลือควาย 1 ตัว อยากทราบว่านกเอี้ยงกี่ตัว
ก. 10 ตัว ข. 8 ตัว
ค. 6 ตัว ง. 4 ตัว
ตอบ ง. 4 ตัว
แนวคิด ให้นกเอี้ยงมี X ตัว และ ควายมี Y ตัว
เกาะตัวต่อตัวเหลือนกเอี้ยง 1 ตัว X – Y = 1 ………..(1)
นกเอี้ยง 2 ตัว เกาะควาย 1 ตัว จะเหลือควาย 1 ตัว Y -
…………(2)
(1)+(2) x -
x = 2
2 = 4
มีนกเอี้ยงอยู่ 4 ตัว
92. ตัดเชือก 25 ฟุต ออกเป็น 2 ท่อน ให้ท่อนแรกเป็น ของท่อนที่สอง อยากทราบว่าท่อนที่สอง
ยาวเท่าไร
ก. 5 ฟุต ข. 10 ฟุต
ค. 15 ฟุต ง. 20 ฟุต
ตอบ ง. 20 ฟุต
แนวคิด ให้เชือกท่อนที่สองยาว X ฟุต ท่อนแรกยาว
ฟุต
X + = 25
= 25
X =
ท่อนที่สองยาว 20 ฟุต
แบบทดสอบ (ค.ร.น. และ ห.ร.ม.)
93. เลขชุดหนึ่งคือ 12 , 4 และ 24 ห.ร.ม. ของเลขชุดนี้คืออะไร
ก. 1 ข. 2
ค. 4 ง. 24
ตอบ ค. 4
![]()
![]() แนวคิด 12 = 2 ´ 2 ´ 3
แนวคิด 12 = 2 ´ 2 ´ 3
4 = 2 ´ 2
24 = 2 ´ 2 ´ 2 ´ 3
2
2 = 4 คือ จำนวนที่หาร 12, 4, 24 ลงตัว ( ห.ร.ม. )
94. จากจำนวน 84, 21 และ 105 จงหา ค.ร.น. ของเลขชุดนี้
ก. 7 ข. 21
ค. 105 ง. 420
ตอบ ง. 420
![]()
![]() แนวคิด 84 = 3 ´ 7 ´ 2 ´ 2
แนวคิด 84 = 3 ´ 7 ´ 2 ´ 2
21 = 3 ´ 7
105 = 3 ´ 7 ´ 5
3
7
5
2
2 = 420 เป็นจำนวนที่ 84 , 21 , 105 หารได้ลงตัว (ค.ร.น.)
95. เลข 2 จำนวน ๆ หนึ่งเป็น 242 จงหาอีกจำนวนหนึ่งเมื่อมีค่า ค.ร.น. เป็น 4,356 และ ห.ร.ม. เป็น 2
ก. 12 ข. 48
ค. 36 ง. 121
ตอบ ค. 36
แนวคิด เลขจำนวนหนึ่ง =
96. ข้อใดคือ ห.ร.ม. ของ 51, 36 และ 81
ก. 1 ข. 3
ค. 36 ง. 5508
ตอบ ข. 3
![]() แนวคิด 51 = 3 ´ 17
แนวคิด 51 = 3 ´ 17
36 = 3 ´ 2 ´ 2 ´ 3
81 = 3 ´ 3 ´ 3 ´ 3
ห.ร.ม. = 3
97. เลขคี่ 2 จำนวนน้อยคือ 35 ถ้า ห.ร.ม คือ 7 และ ค.ร.น. คือ 245 แล้วจำนวนมากคือจำนวนใด
ก. 42 ข. 49
ค. 84 ง. 105
ตอบ ข. 49
แนวคิด 35 = 7 ´ 5
49 = 7 ´ 7
98. เลข 3 จำนวนมี ค.ร.น. เป็น 108 และมี ห.ร.ม. เป็น 9 ถ้าเลข 3 จำนวนนั้น
คือ 27 X และ 108 แล้ว X คือจำนวนใด
ก. 9 ข. 36
ค. 51 ง. 84
ตอบ ก . 9
แนวคิด 27 = 3 ´ 3 ´ 3
9 = 3 ´ 3 ´ 1
108 = 3 ´ 3 ´ 12
ดังนั้น ห.ร.ม. = 3´3 = 9
ค.ร.น. = 3 ´ 3 ´ 1 ´ 12 = 108
99. ถ้า ห.ร.ม. ของเลขชุดหนึ่งเป็น 8 ค.ร.น เป็น 208 ถ้าจำนวนหนึ่งเป็น 104 อีกจำนวนหนึ่งคือ
อะไร
ก. 16 ข. 52
ค. 84 ง. 96
ตอบ ก. 16
แนวคิด 104 = 4 ´ 2 ´ 13
16 = 4 ´ 2 ´ 2
100. เลขชุดหนึ่งประกอบด้วย 8, 32 และ X หารด้วย 4 ลงตัว และนำไปหาร 96 ลงตัวด้วย X คือ
จำนวนอะไร
ก. 12 ข. 25
ค. 36 ง. 40
ตอบ ก. 12
แนวคิด 8 /4 = 2 , 32/4 = 8 , 12/4 = 3 ทั้งสามจำนวนหารด้วย 4 ลงตัว
ดั้งนั้น x = 12 นำไปหาร 96 ได้ 96/12 = 8 ซึ่งหารลงตัวพอดี
 Youpik ขายของออนไลน์
Youpik ขายของออนไลน์
 ธ.กสิกรไทย
ธ.กสิกรไทย

อีเมล : decho.by@hotmail.com
TOP เลื่อนขึ้นบนสุด





